单调栈 题目 1019. 链表中的下一个更大节点 - 力扣(LeetCode)
496. 下一个更大元素 I - 力扣(LeetCode)
503. 下一个更大元素 II - 力扣(LeetCode)
2454. 下一个更大元素 IV - 力扣(LeetCode)
456. 132 模式 - 力扣(LeetCode)
739. 每日温度 - 力扣(LeetCode)
901. 股票价格跨度 - 力扣(LeetCode)
1124. 表现良好的最长时间段 - 力扣(LeetCode)
1475. 商品折扣后的最终价格 - 力扣(LeetCode)
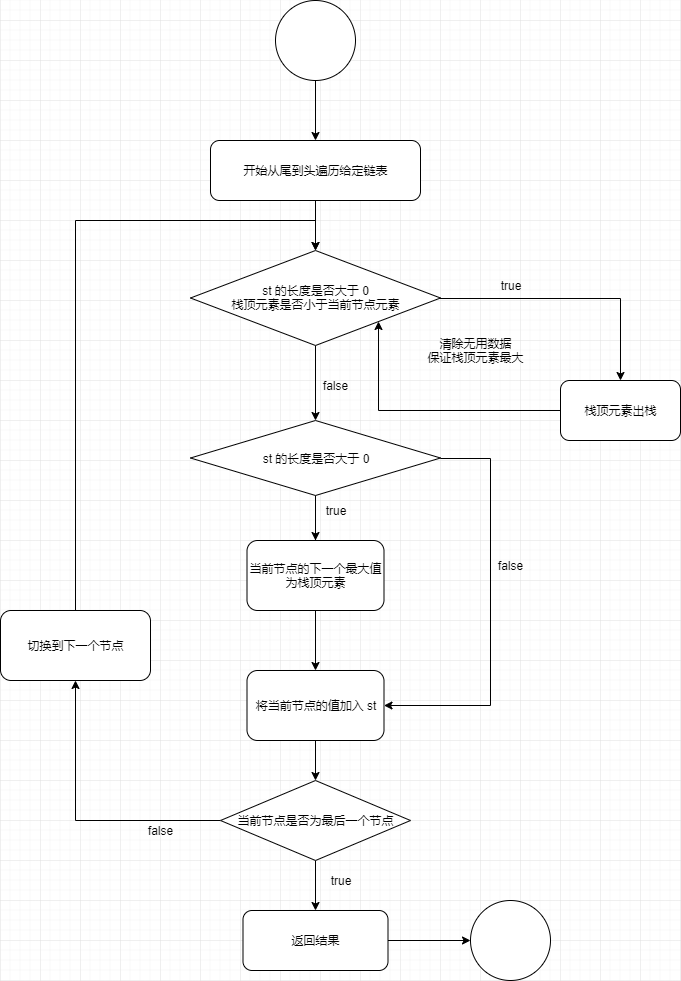
LeetCode 1019 思路流程图 从链表尾部开始向头部遍历(递归或者反转链表都可以)
实现代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 func nextLargerNodes (head *ListNode) int ) { var st = []int {} var f func (*ListNode, int ) f = func (node *ListNode, i int ) if node == nil { res = make ([]int , i) return } f(node.Next, i+1 ) for len (st) > 0 && st[len (st) - 1 ] <= node.Val{ st = st[:len (st) - 1 ] } if len (st) > 0 { res[i] = st[len (st) - 1 ] } st = append (st, node.Val) } f(head, 0 ) return }
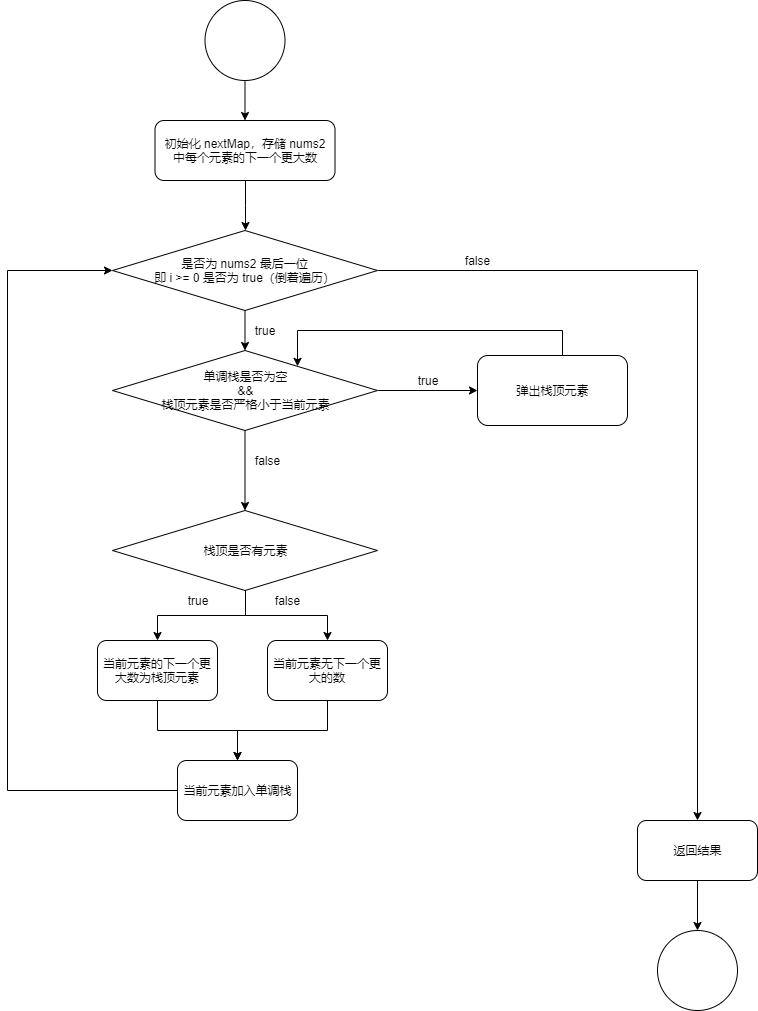
LeetCode 496 思路流程图 和上一个差不多,多了个 map
实现代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 func nextGreaterElement (nums1 []int , nums2 []int ) int { var res = make ([]int , len (nums1)) var nextMap = make (map [int ]int ) var st = []int {} for i := len (nums2) - 1 ; i >= 0 ; i--{ for len (st) > 0 && st[len (st) - 1 ] < nums2[i]{ st = st[:len (st) - 1 ] } if len (st) > 0 { nextMap[nums2[i]] = st[len (st) - 1 ] }else { nextMap[nums2[i]] = -1 } st = append (st, nums2[i]) } for i := range nums1{ res[i] = nextMap[nums1[i]] } return res }
LeetCode 503 思路 是一个循环的数组,只需要两遍单调栈操作就行。
流程图略。
实现代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 func nextGreaterElements (nums []int ) int { var acLen = len (nums) var res = make ([]int , acLen) nums = append (nums, nums...) var st = []int {} for i := len (nums) - 1 ; i >= 0 ; i--{ var nowIndex = i % acLen for len (st) > 0 && st[len (st) - 1 ] <= nums[nowIndex]{ st = st[:len (st) - 1 ] } if len (st) > 0 { res[nowIndex] = st[len (st) - 1 ] }else { res[nowIndex] = -1 } st = append (st, nums[nowIndex]) } return res }
LeetCode 2454 思路 本题用到了两个单调栈,其中与上述代码思路不一样的是
1 2 3 4 5 6 7 var j = len (s) - 1 for j >= 0 && nums[s[j]] < num { j-- } t = append (t, s[j+1 :]...) s = append (s[:j+1 ], i)
j 在 t 中的用处
我们将 s 中弹出的元素压入 t 中,需要保证压入栈时是原有的顺序 。为什么呢,因为 s 是一个单调递减栈,我们在循环一个个出栈时,将栈顶元素一个个压入到 t 中时,t 就变成了一个单调递增栈。这样 s 和 t 的单调性不一样,在进入下一轮遍历时,没有办法顾虑到更小的元素。
举个例子:
1 nums = [11,13,15,12,0,15,12,11,9]
当 i = 5 时(也就是第二个 15),我们会先将下标为 1(也就是元素 13)出栈,然后将压入 0,后压入 12。此时 t 栈的结构为:
在下一轮遍历中(i = 6),12 与栈顶元素 12 比较,发现不满足条件,t 也就不弹栈,导致栈底元素 0 无法与 12 比较,也就找不到下一个更大元素。
当然,在实现中存的是下标,上述只是为了方便理解。
j 在 s 中的用处
for 循环统计了 s 中需要出栈的元素,s = append(s[:j+1], i) 等价于
1 2 s = s[:j+1 ] s = append (s, i)
或者原有逻辑
1 2 3 4 for len (s) > 0 && s[len (s) - 1 ] < num{ s = s[:len (s) - 1 ] } s = append (s, i)
实现代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 func secondGreaterElement (nums []int ) int { var s = []int {} var t = []int {} var res = make ([]int , len (nums)) for i, num := range nums{ for len (t) > 0 && nums[t[len (t) - 1 ]] < num{ res[t[len (t) - 1 ]] = num t = t[:len (t) - 1 ] } var j = len (s) - 1 for j >= 0 && nums[s[j]] < num { j-- } t = append (t, s[j+1 :]...) s = append (s[:j+1 ], i) res[i] = -1 } return res }
LeetCode 456 思路 这题主要多了一个中转数 temp。
要实现 1 3 2 的结构,可以维护一个单调栈(单调递减,底大顶小),在遍历时遇到比栈顶大的元素,出栈,并将出栈元素赋值给 temp。此时 2 和 3 都有了。在每一次遍历时,如果栈内有元素,temp 不为初始值,那么可以比较 temp 和当前元素的差别。如果 temp 大于当前元素(也就是 2 大于 1),那么 132 模式成立,直接返回 true。
这里有一点是,判断当前元素与 temp 的大小在每次出栈操作前边还是后边都不影响。
实现代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 func find132pattern (nums []int ) bool { var st = []int {} var temp int = -1000000001 for i := len (nums) - 1 ; i >= 0 ; i--{ for len (st) > 0 && st[len (st) - 1 ] < nums[i]{ temp = st[len (st) - 1 ] st = st[:len (st) - 1 ] } if len (st) > 0 && nums[i] < temp{ return true } st = append (st, nums[i]) } return false }
LeetCode 739 思路 没啥好讲的,就单调栈。
实现代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 func dailyTemperatures (temperatures []int ) int { var res = make ([]int , len (temperatures)) var st = []int {} for i := len (temperatures) - 1 ; i >= 0 ; i--{ for len (st) > 0 && temperatures[st[len (st) - 1 ]] <= temperatures[i]{ st = st[:len (st) - 1 ] } if len (st) > 0 { res[i] = st[len (st) - 1 ] - i } st = append (st, i) } return res }
LeetCode 901 思路 这道题和之前不一样的点在于,这个距离。如果单调栈内无元素,证明当前元素比之前的所有元素都大(没有元素那它也是最大的),那么只需要返回它的 idx 即可。如果有元素,那就是它左边比它大的第一个元素,idx 相减即可。
实现代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 type StockSpanner struct { idx int data [][2 ]int } func Constructor () return StockSpanner{} } func (this *StockSpanner) int ) int { this.idx++ for len (this.data) > 0 && this.data[len (this.data) - 1 ][1 ] <= price{ this.data = this.data[:len (this.data) - 1 ] } var res int if len (this.data) > 0 { res = this.idx - this.data[len (this.data) - 1 ][0 ] }else { res = this.idx } this.data = append (this.data, [2 ]int {this.idx, price}) return res }
LeetCode 1124 思路 这题和之前不一样的是,用到了前缀和数组。以及求的是 [最长]
我的理解是:
先构造一个前缀和数组,数组中的元素是在这之前 「劳累的天数」 与「不劳累的天数」 的差 。也就是 s[i] = 下标 [0, i) 中劳累的天数与不劳累天数的差。
创建这个前缀和数组时(遍历 hours),维护一个单调递减的单调栈,单调栈在初始化时有一个元素 0(下标)。单调栈内存储的是最长子数组的左端点 。
在计算了当前元素的前缀和后,比较当前前缀和与栈顶元素的大小。如果当前前缀和小于栈顶元素下标表示的前缀和,就将前缀和入栈。为什么呢?如上边说的,单调栈内存储的是最长子数组的左端点 。
代码实现 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 func longestWPI (hours []int ) int { var res int var s = make ([]int , len (hours) + 1 ) var st = []int {0 } for j, hour := range hours{ j++ s[j] = s[j - 1 ] if hour > 8 { s[j]++ }else { s[j]-- } if len (st) > 0 && s[j] < s[st[len (st) - 1 ]]{ st = append (st, j) } } for i := len (hours); i > 0 ; i--{ for len (st) > 0 && s[i] > s[st[len (st) - 1 ]]{ res = max(res, i - st[len (st) - 1 ]) st = st[:len (st) - 1 ] } } return res } func max (x,y int ) int { if x > y{ return x } return y }
LeetCode 1475 思路 没啥好说的,单调递增栈
实现代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 func finalPrices (prices []int ) int { var res = make ([]int , len (prices)) var st = []int {} for i := len (prices) - 1 ; i >= 0 ; i--{ for len (st) > 0 && st[len (st) - 1 ] > prices[i]{ st = st[:len (st) - 1 ] } if len (st) > 0 { res[i] = prices[i] - st[len (st) - 1 ] }else { res[i] = prices[i] } st = append (st, prices[i]) } return res }
Reference & Thanks 灵神的单调栈题单
496. 下一个更大元素 I - 力扣官方题解
2454. 下一个更大元素 IV - 灵茶山艾府的题解
456. 132 模式 - 宫水三叶的题解
901. 股票价格跨度 - 力扣官方题解
1124. 表现良好的最长时间段 - 灵茶山艾府的题解